ベンフォード分析は一般的には聴き慣れない名称ではありますが、監査の現場では監査ツールとして監査ソフトウエアに組み込まれており、その分析はコマンド機能を操作する事で容易にグラフを描けることができます。
下図は2018年3月2月の香港上場銘柄の終値(1596銘柄)の頭２桁がどのような数字となっているかを抜き出したものです。ここで株価の数値を出す事に特別な意味はなく、自然界に存在しているランダムな数値のサンプルとして抜き出したに過ぎません。縦軸が件数、横軸が２桁の数字(10～99)のグラフとなっています。緑色の棒グラフは実績値の件数で、赤色の曲線はベンフォードの法則で計算される予測値を示しており、株価の頭2桁の数値分布はベンフォードの法則の期待分布とほぼパラレルな状況となっている事が分かります。

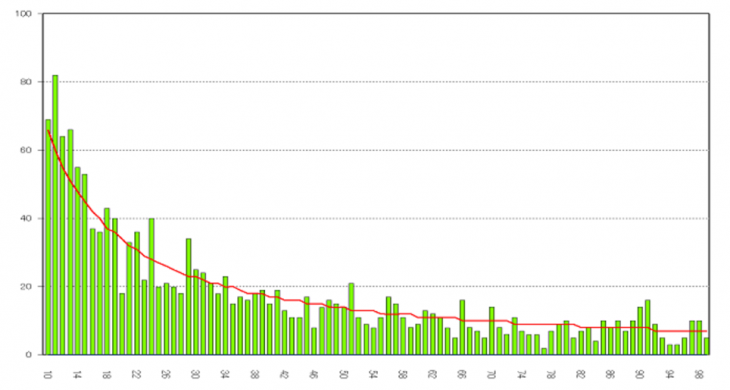
ベンフォード(Benford)の法則とは、いったいどのようなものか？
自然界に存在しているランダムな数値(10進数)の1桁目の数値の出現確率分布には、均等ではない偏りが存在しており、1桁目が1の時の出現確率が最も大きく、 1桁目の数値が増えるに従い出現確率が減少していくことが観測されるという法則です。これは2桁の数値(10から99まで)でも同様で、11の時の出現確率が最多で数値が増加するごとに発生頻度は低下していきます。

◆ベンフォードの法則による数値の発生頻度：1桁の場合

ベンフォードの法則の存在は、古くから広く知られており,会計･監査以外の様々な分野での利用研究も数多く報告されています。「自然界に存在しているランダムな数値」とは、上記で述べた株価以外でも、都市の人口、年間降水量など様々なデータが対象となりますが、実際に適用できない条件下のデータもあります。
・郵便番号や車のナンバープレートのように割り当てられた数字
・価格マスタ等、人為的に設定されたマスタデータ
・予め最小限と最大値が定められたレンジが存在するデータ

そしてこの法則は、会計数値を含むデータの異常性の有無を検証する為の不正検出手法として利用されます。下図の通り前例で挙げた香港上場株式の株価は、頭1桁目の数値分布においても極端に小さい数値の方向に歪んだ対数分布となっていますが、これは期待値分布とそれほど乖離していませんので正常な分布であると言えます。逆に言うと数値分布が、もしこの歪んだ形状からかけ離れていたとすれば、その数値は自然な数値分布ではない可能性があるということになります。

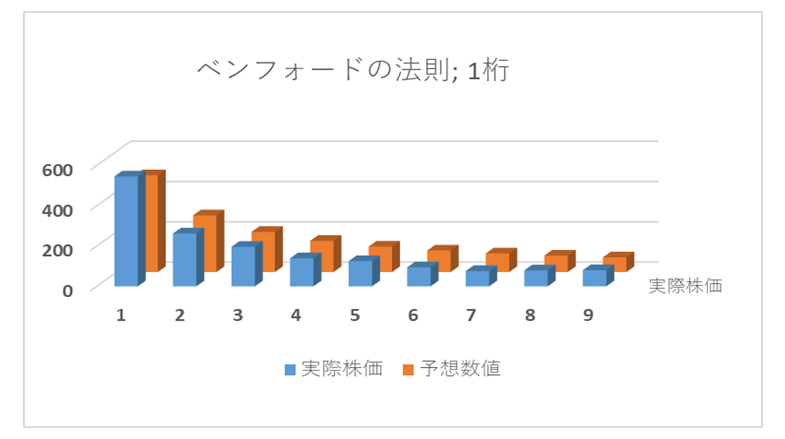
仮に経理伝票等に記入された数値データに対して担当者が意図的な操作を加えた場合、例え正常な分布を装っていても集計した数値データの桁別の数値分布は、ベンフォードの法則の期待分布から何らかの突出した乖離が観察されることが予想されます。すなわち『人間は、ランダム性の欠如する数値を無意識に作成してしまいがち』であり『ランダムな数値を作成しているつもりでも、実際には習慣・気質・好み等が反映し、数値にゆがみを与えるもの』となってしまうからです。
予期しないスパイク(突出値)または下落が発生した場合、ドリルダウンする事により内容を精査し、サンプル数を増やすなどして異常値を更に検証していく必要があります。
　
最近では、ベンフォード分析は財務諸表の数値のみならず様々な分野で適用されており、選挙投票の集計結果・税務還付申告書の数字･アンケート調査データ･大気汚染の観測値等に至るまでの様々なデータに潜むデータの改ざんや提造の可能性を統計的に検証する為に利用されています。